Premium status ti omogućava:






Otključaj prelaskom na
premium nalog.

Osvoj Premium 10 min besplatno
Uradi dnevne zadatke i
dobićeš pristup
Premium
sadržaju na 10 min
Idi na
Shtreberove lekcije proizvod su puno rada i istraživanja. Podržite nas kupovinom Premium naloga i omogućite vašem detetu da uči na najbolji način. Hvala!
Kupi sada Računsku operaciju deljenja matematičkim jezikom zapisujemo:
Zapis a: b = q (r) se drugačije može zapisati kao
Podeli broj 23 brojem 5.
Rešenje
23 : 5 = 4 (3)
PRAVILNO je pisati ostatak u zagradi pored količnika.
*** VODI RAČUNA ***
Ukoliko se umesto zagrade stavi zapeta dobija se broj koji se zove DECIMALAN BROJ koji se razlikuje od našeg broja. O ovim brojevima ćemo učiti u narednim lekcijama.
Broj a je deljiv brojem b ukoliko se prilikom deljenja ne dobije ostatak.
*Tačnije, ostatak pri deljenju broja a sa brojem b je 0.
OSTATAK: Broj koji se javlja pri deljenju celih brojeva...

Otključaj Premium
 Čitaj celu lekciju
Čitaj celu lekciju
 Rešavaj 10x više zadataka
Rešavaj 10x više zadataka
 Osvoj 2x više bodova i energija ti se puni duplo brže
Osvoj 2x više bodova i energija ti se puni duplo brže
Za 1200 RSD postani Premium!
Postani PremiumKada je broj a deljiv brojem b može se takođe reći da broj b deli broj a. Matematičkim jezikom se to piše b | a.
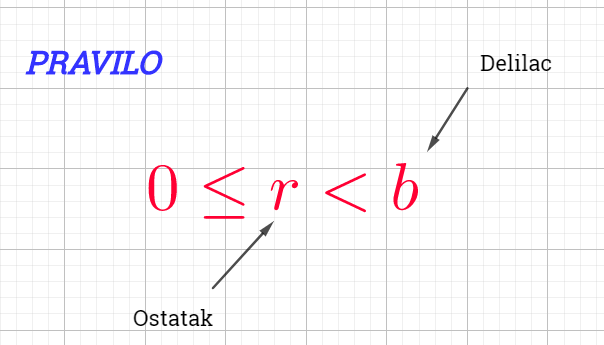
Ostatak je uvek veći ili jednak sa nulom, a manji od delioca.
Ako je ostatak pri deljenju broja a sa brojem b jednak 0, broj a je deljiv brojem b, a ako je ostatak pri tom deljenju veći od 0, broj a nije deljiv brojem b.
Kao deljenik, broj nula je deljiv bilo kojim prirodnim brojem.
Nula ne sme da bude delilac.

Nulom ne sme da se deli.

Svojstvo 1. Ako su sabirci deljivi nekim brojem, onda je i zbir deljiv tim brojem.
Primer
Broj 6 deli brojeve 18 i 12. Po pravilu deljivosti broj 6 deliće i njihov zbir. Tačnije,
18 + 12 = 30
6|18 i 6|12, pa 6|30.
Svojstvo 2. Ako su umanjenik i umanjilac deljivi nekim brojem, onda je i razlika deljiva tim brojem.
Primer
Broj 6 deli brojeve 18 i 12. Po pravilu deljivosti broj 6 deliće i njihovu razliku. Tačnije,
18 - 12 = 6
6|18 i 6|12, pa 6|6.
Svojstvo 3. Ako je jedan činilac proizvoda deljiv nekim brojem (s | a ili s | b), onda je i proizvod deljiv tim brojem (s | a ∙ b).
Primer
Broj 3 deli broj 15, ali broj 3 ne deli broj 4. Međutim, po pravilu deljivosti ukoliko neki broj deli jedan od činilaca, deliće i njihov proizvod.
i
, pa
Svojstvo 4. Za bilo koja tri prirodna broja a, b i s ako a | b i b | c onda a | c.
Primer
U srednjoj školi ovo svojstvo će se zvati TRANZITIVNOST.
Ako 5 deli 25, a 25 deli 100, onda će 5 deliti 100.
Delioci broja A su svi prirodni brojevi koji DELE broj A.
Delioci broja A se navode kao skup
Broj 1 je delilac bilo kog prirodnog broja.
Skup delilaca je konačan skup.
Primer 1.
Navedi sve delioce broja 9.
Rešenje:
Primer 2.
Navedi sve delioce broja 20.
Rešenje:
Sadržaoci broja A su svi brojevi koji mogu da se podele brojem A. Tačnije, to su brojevi koji SADRŽE broj A.
Sadržaoci skupa A se navode kao skup
Svi prirodni brojevi su sadržaoci broja 1.
Skup sadržalaca nekog broja je beskonačan.
Primer 1.
Navedi sadržaoce broja 4.
Rešenje:
Primer 2.
Navedi sadržaoce broja 15.
Rešenje:
Broj je deljiv dekadnom jedinicom ukoliko se završava sa bar onoliko nula koliko ta dekadna jedinica ima nula.
Preciznije:
Ako se zapis prirodnog broja završava cifrom 0 deljiv je sa 10.
Ako se zapis prirodnog broja završava sa dve cifre 0 deljiv je sa 100.
Ako se zapis prirodnog broja završava sa tri cifre 0 deljiv je sa 1000.
Primer
Broj 74850 je deljiv brojem 10, jer se broj 74850 završava cifrom 0.
Broj 74850 nije deljiv brojem 100, jer se završava ciframa 5 i 0, a da bi bio deljiv brojem 100 mora da se završava sa 00.
Broj je deljiv brojem 2 ako je paran.
Preciznije, broj je deljiv brojem 2 ako se završava ciframa 0, 2, 4, 6 ili 8.
Primer
Broj 745 nije deljiv brojem 2 pošto je 745 neparan broj (završava se cifrom 5).
Broj 548 je deljiv brojem 2 pošto je 548 paran broj (završava se cifrom 8).
Broj je deljiv brojem 5 ako se završava ciframa 0 ili 5.
Primer
Broj 328 nije deljiv brojem 5, pošto se broj 328 završava cifrom 8.
Broj 545 je deljiv brojem 5, pošto se 545 završava cifrom 5.
Broj je deljiv brojem 4 ako je dvocifreni završetak tog broja deljiv sa 4.
Preciznije, broj je deljiv brojem 4 ako se završava sa 00, 04, 08, 12, 16, 20, 24, 32 i slično.
Primer
Broj 825 nije deljiv brojem 4, jer se završava sa 25, a 25 nije deljivo sa 4.
Broj 548 je deljiv brojem 4, jer je 48 deljivo sa 4.
Broj je deljiv brojem 25 ako je dvocifreni završetak tog broja deljiv sa 25.
Preciznije, broj je deljiv brojem 4 ako se završava sa 00, 25, 50 i 75.
Primer
Broj 825 je deljiv brojem 25, jer se završava sa 25.
Broj 548 nije deljiv brojem 25, jer 48 nije deljivo sa 25.
Broj je deljiv brojem 25 ako je dvocifreni završetak tog broja deljiv sa 25.
Preciznije, broj je deljiv brojem 4 ako se završava sa 00, 25, 50 i 75.
Primer
Broj 825 je deljiv brojem 25, jer se završava sa 25.
Broj 548 nije deljiv brojem 25, jer 48 nije deljivo sa 25.
Broj je deljiv brojem 3 ukoliko je zbir cifara tog broja deljiv sa 3.
Primer
Broj 1234 nije deljiv brojem 3, jer je zbir cifara ovog broja 1+2+3+4=10, a 10 nije deljiv sa 3.
Broj 11100306 je deljiv brojem 3, jer je zbir cifara ovog broja 1+1+1+0+0+3+0+6=12, a 12 je deljiv sa 3.
Broj je deljiv brojem 9 ukoliko je zbir cifara tog broja deljiv sa 9.
Primer
Broj 1234 nije deljiv brojem 9, jer je zbir cifara ovog broja 1+2+3+4=10, a 10 nije deljiv sa 9.
Broj 1800306 je deljiv brojem 3, jer je zbir cifara ovog broja 1+8+0+0+3+0+6=18, a 18 je deljiv sa 9.
* Broj je deljiv sa 6 ako je deljiv sa 2 i 3.
* Broj je deljiv sa 15 ako je deljiv sa 3 i 5.
* Broj je deljiv brojem 20 ako je deljiv sa 4 i 5.
Na ovaj način možemo da proverimo deljivost svim brojevima koji mogu da se dobiju kao proizvod brojeva 2, 3, 4, 5, 9, 25, 10, 100 itd.
Primer
Da li je broj 171230 deljiv brojem 60?
Rešenje:
Da bi broj bio deljiv brojem 60 mora da bude deljiv brojevima 2,3 i 10 jer je
Broj 171230 je deljiv brojem 2 jer je paran, deljiv je brojem 10 jer se završava cifrom 0, ali nije deljiv sa 3 jer je zbir cifara 1+7+1+2+3+0=14, a 14 nije deljiv sa 3.
Prema tome, broj 171230 nije deljiv sa 60.
Broj je deljiv sa 11 kada je razlika između zbira cifara (jednocifrenih klasa) koje stoje na neparnim i onih koje stoje na parnim mestima deljiva sa 11.
***lakše se pamti***
Da li je broj ABCD deljiv sa 11?
Ovaj broj će biti deljiv sa 11 ako je A-B+C-D deljiv sa 11.
Dakle, naizmenično stavljaš znake - i + i izračunaš rezultat. Ako je rezultat deljiv sa 11, onda će i sam broj biti deljiv sa 11.
Primer
Da li je broj 8684016 deljiv sa 11?
Hajde da provermo.
8-6+8-4+0-1+6=2+4+0-1+6=6-1+6=5+6=11
11 je deljivo sa 11, pa je broj 8684016 deljiv sa 11.
Broj je deljiv sa 7, 13, 77, 91, 143 i 1001 kada je razlika između zbira trocifrenih klasa koje u broju stoje na neparnim mestima i zbira trocifrenih klasa koje stoje na parnim mestima deljiva sa datim od brojeva.
***lakše se pamti***
Da li je broj ABCDEFGHI deljiv sa 7, 13, 77, 91, 143 i 1001?
Ovaj broj će biti deljiv sa 7, 13, 77, 91, 143 i 1001 ako je ABC-DEF+GHI deljiv sa 7, 13, 77, 91, 143 i 1001.
Dakle, naizmenično stavljaš znake - i + kod trocifrenih klasa i izračunaš rezultat. Ako je rezultat deljiv sa 7, 13, 77, 91, 143 i 1001, onda će i sam broj biti deljiv sa 7, 13, 77, 91, 143 i 1001.
Primer
Da li je broj 739 693 385 deljiv sa 7, 13, 77, 91, 143 i 1001?
739 - 693 + 385 = 46 + 385 = 431
Broj 431 nije deljiv ovim brojevima, pa nije ni 739 693 385.
Primer
Da li je broj 86 415 deljiv sa 7?
86 je dvocifrena klasa i možemo ispred nje staviti 086 to je na neparnom mestu, a 415 je na parnom.
86 – 415 ne znamo da izračunamo (gradivo šestog razreda), pa radimo 415-86=329
Broj 329 je deljiv sa 7, pa je i broj 86 415 deljiv sa 7.
Broj je deljiv sa 8 kada je trocifren završetak deljiv sa 8.(npr. 123456016:8=15432002)
Broj je deljiv sa 16 kada je četvorocifren završetak deljiv sa 16. (npr. 123450016:16=7715626)
1. Odredi skup svih delilaca broja 142.
2. Odredi skup sadržalaca broja 17.
3. Iz skupa brojeva Y = {5, 8, 9, 10, 11, 12, 14, 15, 16, 18, 20, 21, 23, 24} izdvoj:
1) podskup brojeva deljivih sa 2
2) podskup brojeva deljivih sa 3
3) podskup brojeva deljivih sa 4
4) podskup brojeva deljivih sa 5
5) podskup brojeva deljivih sa 9
6) podskup brojeva deljivih sa 10.
4. Ne izračunavajući zbir i razliku proveri da li je broj 135+225-15 deljiv sa 3 i sa 5.
5. Koje cifre možemo staviti umesto * da bi broj bio deljiv sa 3.
NAPOMENA
Crta iznad broja 15*7 znači da je ovaj broj četvorocifren, ako bi pisalo to znači da je 7a1 trocifren broj. Ova crta se piše da se ne bi pomislilo da je to proizvod ovih brojeva.
U matematici, ukoliko se napiše 7a1 podrazumeva se kao da piše , pa ako želimo da naglasimo da to nije množenje već trocifreni broj, onda pišemo crtu iznad.