Premium status ti omogućava:






Otključaj prelaskom na
premium nalog.

Osvoj Premium 10 min besplatno
Uradi dnevne zadatke i
dobićeš pristup
Premium
sadržaju na 10 min
Idi na
Shtreberove lekcije proizvod su puno rada i istraživanja. Podržite nas kupovinom Premium naloga i omogućite vašem detetu da uči na najbolji način. Hvala!
Kupi sadaОСЦИЛАТОРНОТО ДВИЖЕЊЕ
Во минатата лекција научивме што е осцилаторно движење,осцилација,периодично икружно движење.
Во оваа лекција ќе дефинираме уште три нови поими и тоа:
Растојанието меѓу рамнотежната положба и најоддалечената положба до која стигнува телото при осцилаторното движење е АМПЛИТУДА НА ОСЦИЛИРАЊЕ.
Во примерот подолу тоа е движењето до точката А и Б до кои лулашката стигнува откако ќе помине низ рамнотежната положба О (максималното оддалечување од рамнотежната положба).
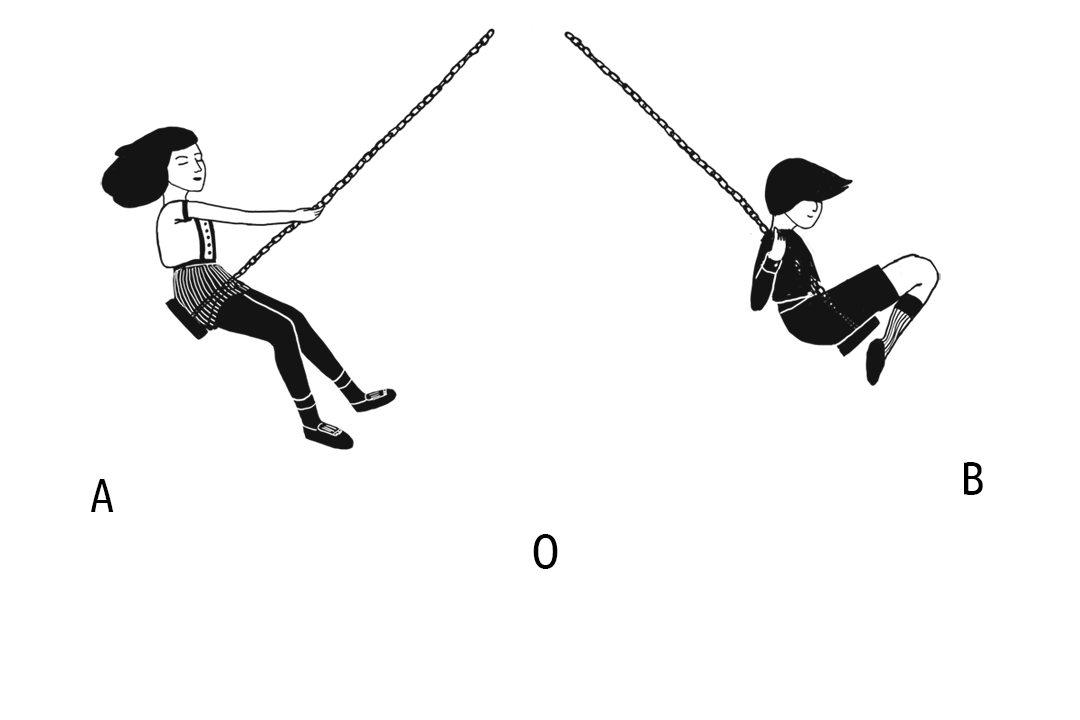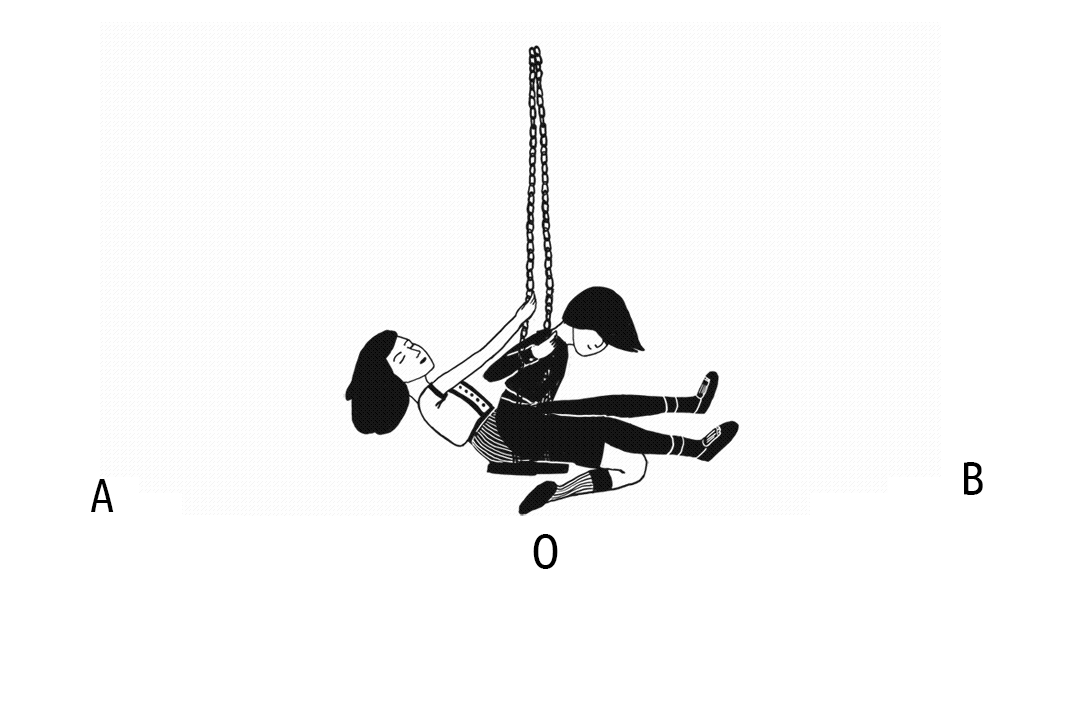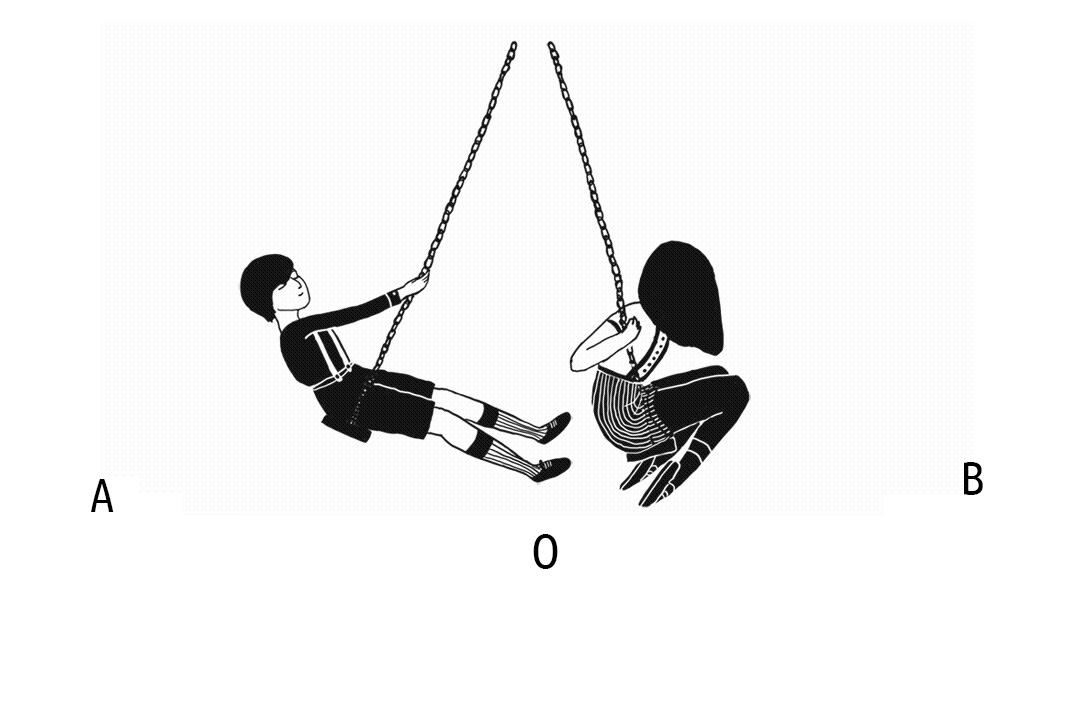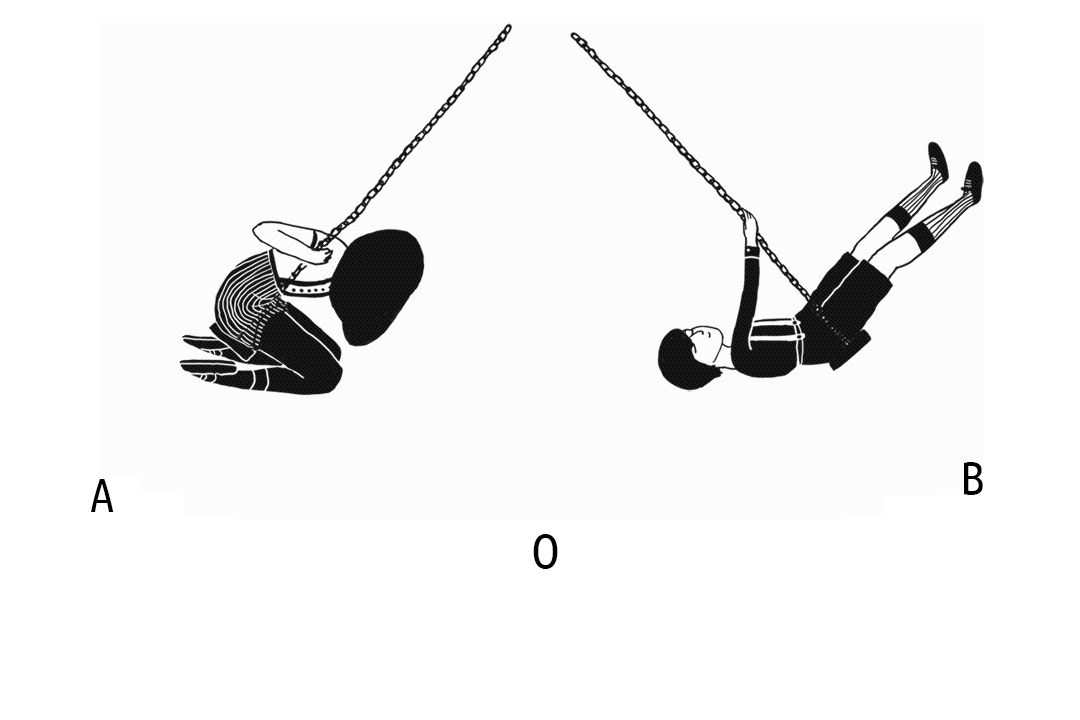
Кога нашата лулашка ќе го помине патот од А преку О до Б и ќе се врати до положбата А, извршила една ЦЕЛА ОСЦИЛАЦИЈА.
АМПЛИТУДА
Пример за амплитуда имаме и на следната слика:

Во точката О е рамнотежната положба (положбата на неистегнатата спирала), а во точките А1 и А2 се амплитудите. Кое било растојание меѓу точките А1 и А2 се нарекува елонгација.
Елонгацијата е кое било растојание од рамнотежната положба во кој било момент од осцилирањето.

Otključaj Premium
 Čitaj celu lekciju
Čitaj celu lekciju
 Rešavaj 10x više zadataka
Rešavaj 10x više zadataka
 Osvoj 2x više bodova i energija ti se puni duplo brže
Osvoj 2x više bodova i energija ti se puni duplo brže
Za 1200 RSD postani Premium!
Postani PremiumПЕРИОДОТ НА ОСЦИЛИРАЊЕ
Веќе кажавме дека кога телото ќе го помине патот од А1 до А2 и назад до А1, тоа извршило една цела осцилација.
ПЕРИОДОТ НА ОСЦИЛИРАЊЕ е времето за кое телото извршува една цела осцилација и се обележува со Т.
Мерна единица на периодот на осцилирање е секунда (ѕ).
Нека телото направило n цели осцилации за време t, тогаш периодот на осцилирање Т на ова тело го пресметуваме како:
Т = t / n
Т – период на осцилирање
t – време на осцилирање
n – број на осцилации во набљудуваното време

Бројот на осцилациите во една секунда се нарекува ФРЕКВЕНЦИЈАили ЗАЧЕСТЕНОСТ на осцилирањето.
ФРЕКВЕНЦИЈАТА се обележува со малата грчка буква (ni) - V. Единицата е Hz – (се чита херц)
Нека телото направило n цели осцилации за време t, тогаш фреквенцијата на ова тело ја пресметуваме како:
V = n/t

Постои уште една формула за одредување на фреквенцијата. Кога ни е познат периодот на осцилирање лесно ни е да ја пресметаме фреквенцијата. Затоа што фреквенцијата е еднаква на реципрочната вредност на периодот на осцилирање:

Врз основа на формулата во претходниот блок, едноставно можеме да изведеме и на што е Hz еднаков:
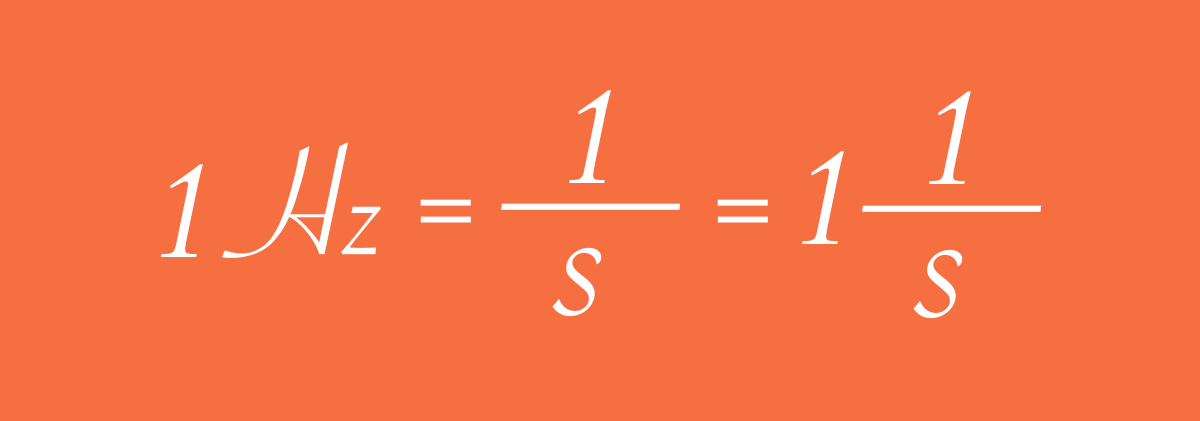
Лекарот изброил 77 отчукувања на Вашето срце во минута.
Колкав е периодот и фреквенцијата на осцилирање на срцето?
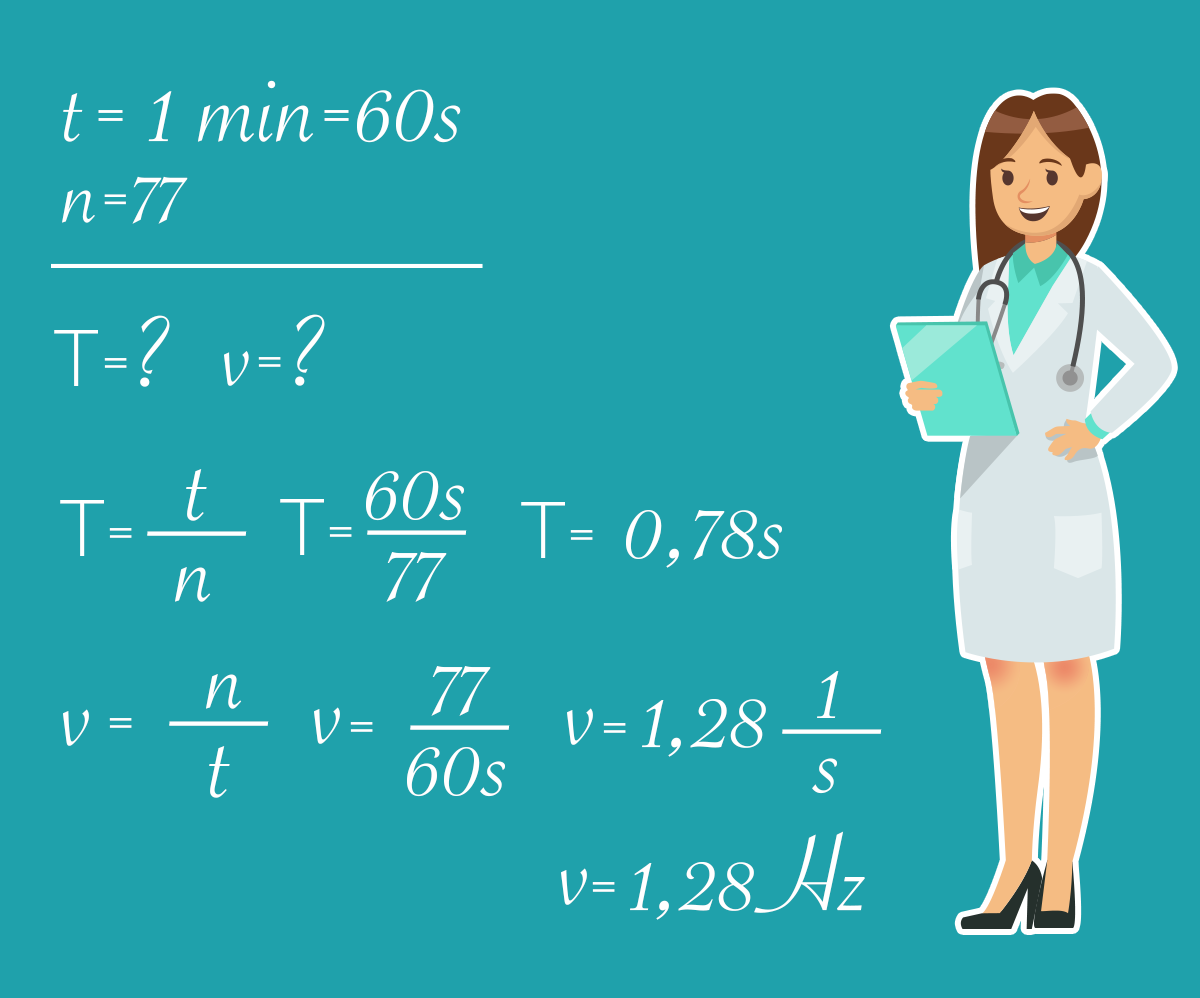
МАТЕМАТИЧКО НИШАЛО
Нишало е секое тело кое е врзано со јаже (нерастеглива нишка) и пуштено кон долу и може да осцилира во вертикална рамнина.
На него дејствува силата на земјината тежа Fg и силата на затегнување на јажето.
Кога таквото тело ќе го извадиме од рамнотежната положба (ќе го занишаме), тоа ќе почне да се движи.
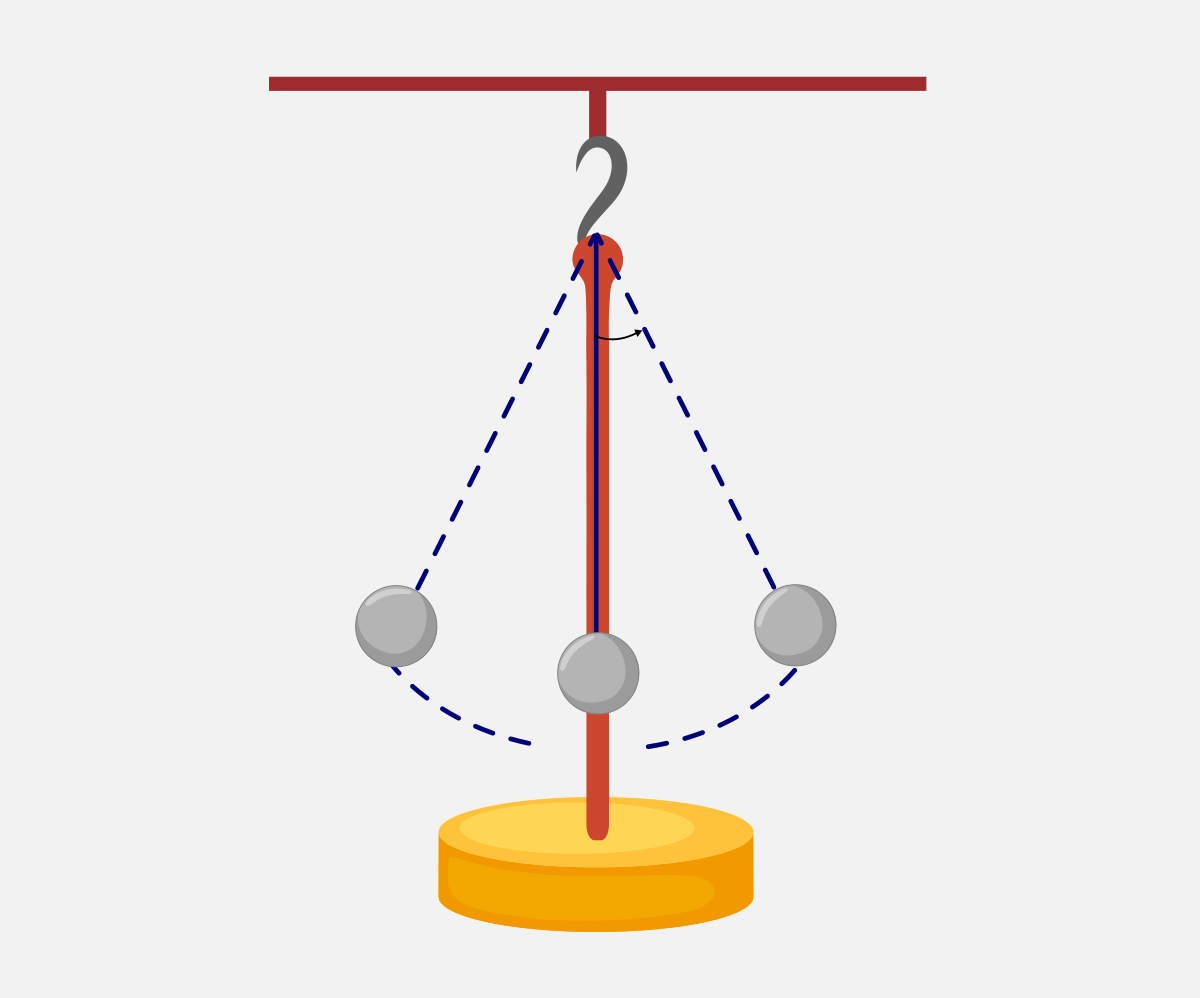
Тоа движење е периодично, осцилаторно околу својата рамнотежна положба.
Најчесто за нишало земаме мало метално топче закачено на танок конец – за ваквото нишало велиме дека има мал или занемарливо мал отпор од воздухот.
Должината на конецот од топчето до точката каде што е врзано се нарекува ДОЛЖИНА НА НИШАЛОТО.
Велиме дека МАТЕМАТИЧКО НИШАЛО е она кај кое топчето е занемарливо мало, т.е. чиј дијаметар е занемарлив во однос на должината на конецот и има занемарливо мала маса.
На пример, нишка со должина од 1 m и топче со дијаметар од 1 cm прават математичко нишало, но нишка со иста должина и топче со дијаметар од 10 cm не прават математичко нишало.
Реално е невозможно да постои совршено математичко нишало.
Со помош на математичкото нишало можеме да го пресметаме забрзувањето на силата на Земјината тежа.
Периодот на осцилирање на математичкото нишало се смета по посебна формула, а тоа е:
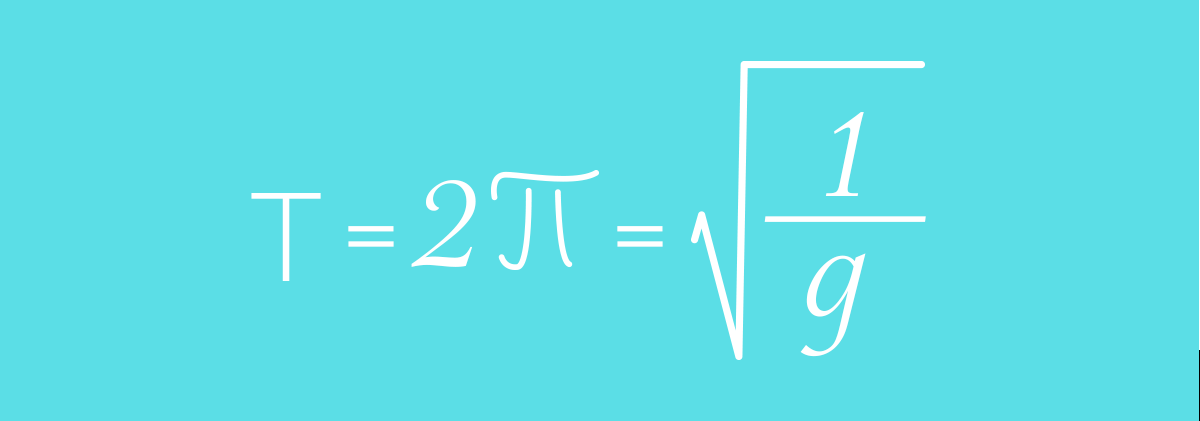
Со оглед на тоа што знаеме дека π е константа која изнесува приближно 3,14, а g – забрзување на земјината тежа 9,81 m/s2 доаѓаме до заклучок дека периодот на математичкото нишало при мали амплитуди зависи само од должината на нишалото.