Premium status ti omogućava:






Otključaj prelaskom na
premium nalog.

Osvoj Premium 10 min besplatno
Uradi dnevne zadatke i
dobićeš pristup
Premium
sadržaju na 10 min
Idi na
Shtreberove lekcije proizvod su puno rada i istraživanja. Podržite nas kupovinom Premium naloga i omogućite vašem detetu da uči na najbolji način. Hvala!
Kupi sadaПОТЕНЦИЈАЛНА ЕНЕРГИЈА
Во минатата лекција научивме што е тоа математичко нишало.
Исто така, треба да се потсетиме дека потенцијална енергија (Ep) имаат телата кои се наоѓаат на некоја висина или ако се оддалечени од рамнотежната положба и Ep зависи од висината и масата на телото.
Ep = mgh.
КИНЕТИЧКАТА ЕНЕРГИЈА
Да се потсетиме и на кинетичката енергија (Ek).
Кинетичка енергија имаат само телата кои се движат и Ek зависи само од масата и брзината на движење на телото
Ek= m·v^2/2.
Ќе анализираме како се менуваат енергиите на математичко нишало и на еластична спирала (правилно би било да се каже систем тело – спирала) во текот на осцилирањето.
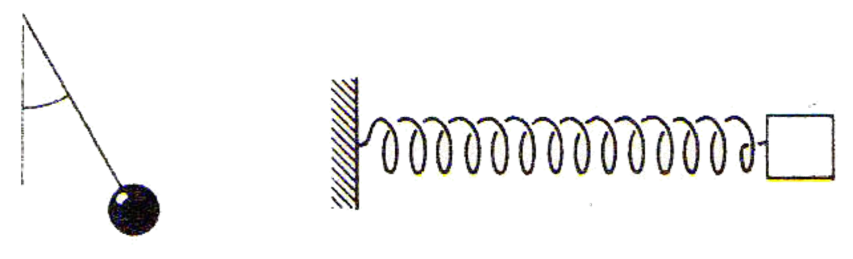
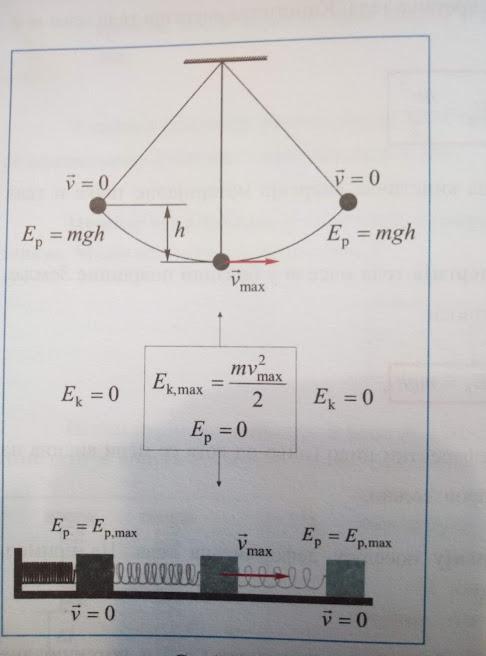
Во крајната десна положба топката на нишалото мирува и тогаш има само потенцијална енергија, затоа што има висина во однос на рамнотежната положба.
Кинетичката енергија на нишалото во оваа точка е нула, затоа што брзината му е нула.
Слично е и со спиралата, само што тука станува збор за еластична потенцијална енергија. Таа е максимална, затоа што спиралата е максимално развлечена.
Кога ќе го пуштиме топчето, висината се намалува, што значи дека се намалува и потенцијалната енергија, а кинетичката енергија расте, бидејќи расте и брзината на топчето. Така е и со телото на спирала. Брзината на топчињата се зголемува под дејство на гравитациските сили, а брзината на телото на спирала под влијание на еластичните сили.
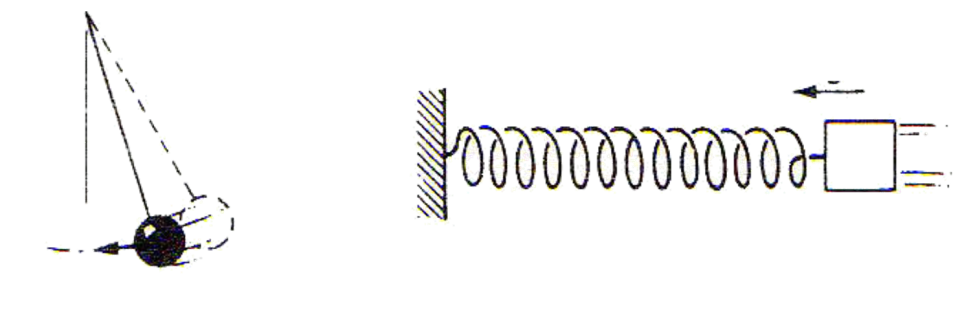
Во рамнотежна положба брзината на двете тела се максимални, па и нивните кинетички енергии. Потенцијалните енергии им се нула.
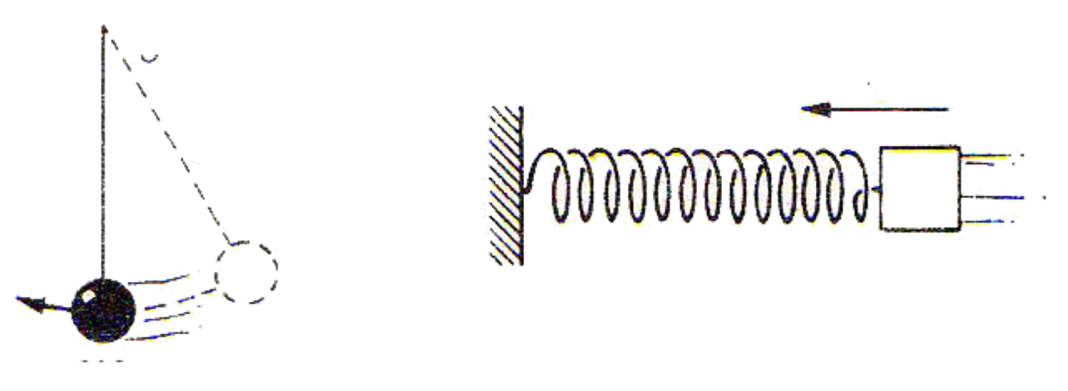
Телата продолжуваат да се движат, но сега забавено. Потенцијалната енергија на двете тела почнува да расте (со оддалечувањето на телото од рамнотежната положба, бидејќи висината расте), а кинетичката енергија сè повеќе се намалува (со намалувањето на брзината).
Во крајната лева положба на топката нишалото мирува и повторно има само потенцијална енергија. Кинетичката енергија на нишалото во оваа точка е нула. Потенцијалната енергија на телото на спирала е најголема затоа што спиралата е максимално збиена.
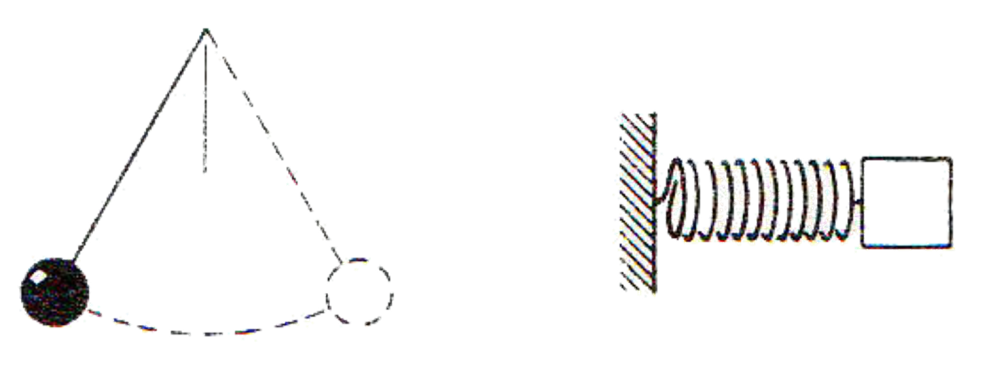
Телата продолжуваат да се движат, но сега забрзано. Потенцијалната енергија на двете тела почнува да опаѓа, а брзината (кинетичката енергија) да расте.
Во рамнотежната положба е сè исто како и во претходната анализа, само телата се движат во спротивна насока.
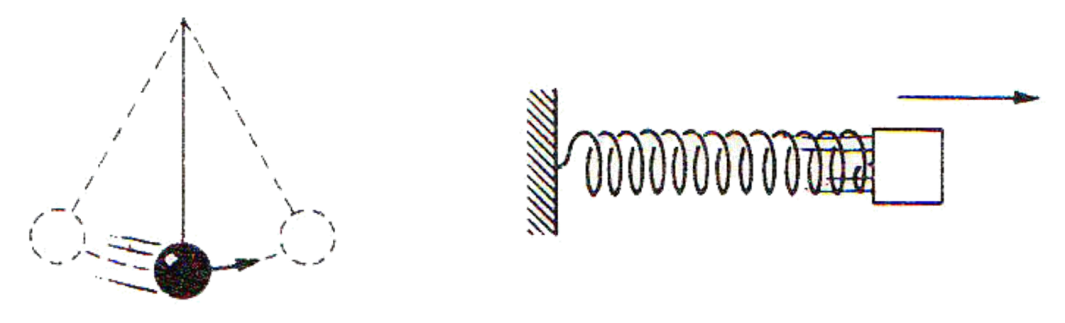
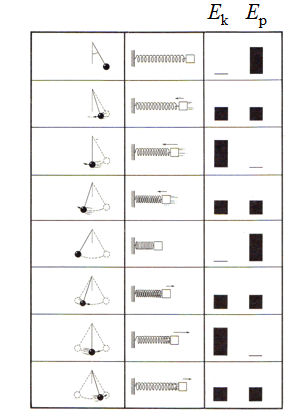
Анализата на енергијата на математичкото нишало и на еластичната спирала може многу ефектно да се прикаже на следниот начин.

Otključaj Premium
 Čitaj celu lekciju
Čitaj celu lekciju
 Rešavaj 10x više zadataka
Rešavaj 10x više zadataka
 Osvoj 2x više bodova i energija ti se puni duplo brže
Osvoj 2x više bodova i energija ti se puni duplo brže
Za 1200 RSD postani Premium!
Postani PremiumЕНЕРГИЈА НА НИШАЛОТО (на уште еден начин)
За нишалото да почне да осцилира мораме да го изместиме од рамнотежната положба. Тоа ќе го направиме така што ќе вложиме МЕХАНИЧКА РАБОТА, а нишалото ќе ја добие потребната енергија и ќе почне да се движи.
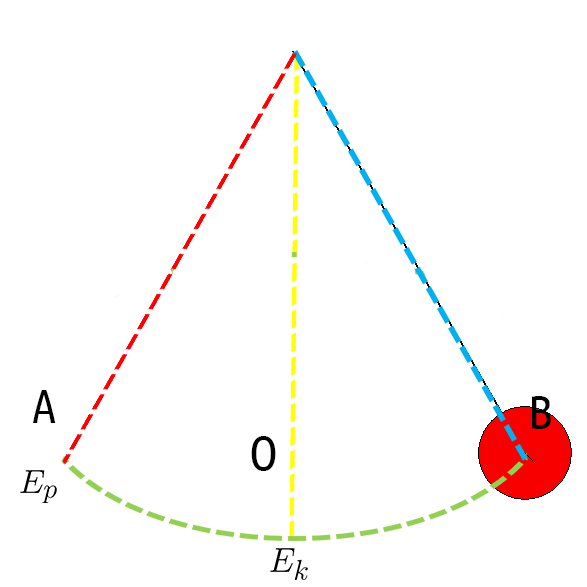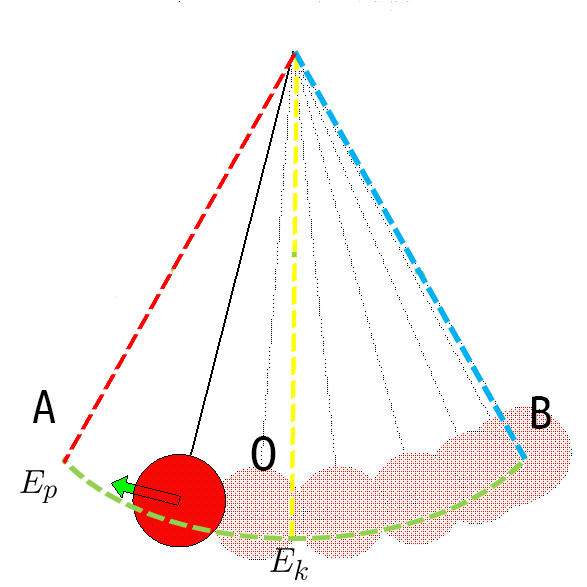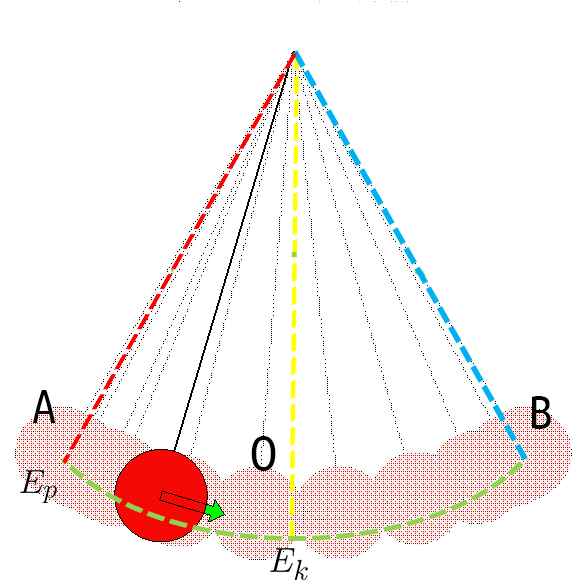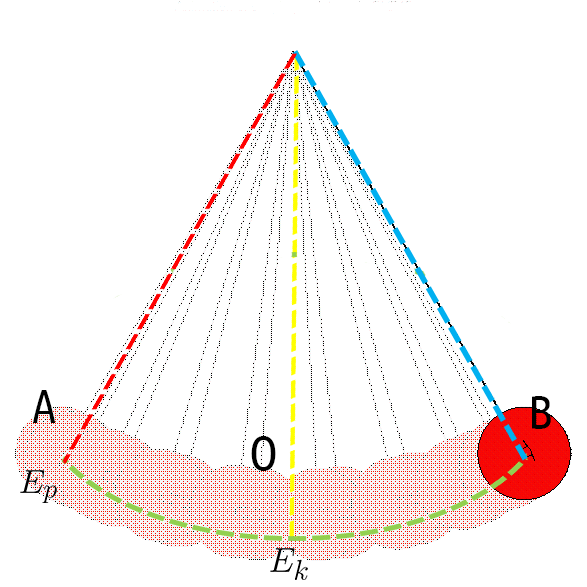
Кога топката се наоѓа во крајната положба А или Б, таа за момент мирува и тогаш има само потенцијална енергија, меѓутоа кога ќе тргне да се спушта, оди кон рамнотежната положба. Кога ќе дојде до точката О, нашата топка има само кинетичка енергија.
ЕНЕРГИЈА НА ЕЛАСТИЧНА СПИРАЛА (на уште еден начин)
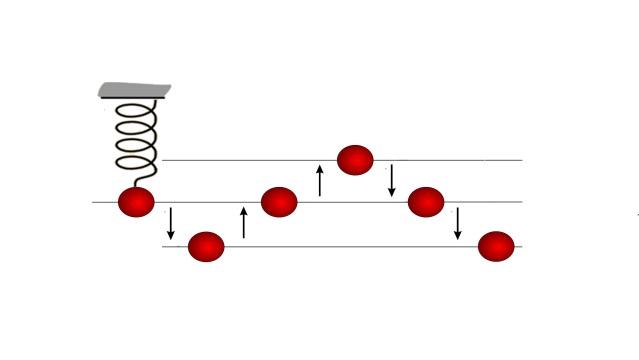
Ова е пример за една топка која е закачена на еластична спирала. Ако ја повлечеме топката надолу и ја растегнеме спиралата, топката ќе почне да се движи осцилаторно како на сликата.
Кога е максимално оддалечена од рамнотежната положба, топката има исклучиво ПОТЕНЦИЈАЛНА ЕНЕРГИЈА, затоа што тогаш за момент се наоѓа во состојба на релативно мирување.
Но, кога спиралата повторно ќе ја придвижи, топката почнува да се движи кон својата рамнотежна положба, добива забрзување и во рамнотежната положба има исклучиво КИНЕТИЧКА ЕНЕРГИЈА.
ЗАКОН ЗА ОДРЖУВАЊЕ НА МЕХАНИЧКАТА ЕНЕРГИЈА
Врз основа на сето напишано, се изведува заклучок дека вкупната енергија не се менува, туку само преминува од потенцијална во кинетичка и обратно, а еднаква е на збирот на овие две енергии.
E = Ep + Ek=const
Ова воедно претставува и Закон за одржување на механичката енергија.
Овој Закон за одржување на механичката енергија на телото преку формули може да се претстави како:
Постојат уште два типа на осцилации кои ќе се обработуваат во средно училиште, а тоа се: